新闻动态
统计咨询介绍 | R程序包SLFPCA:二值函数型数据的稀疏主成分估计
时间:2021-10-01一、什么是SLFPCA?
函数型主成分分析(Functional principal component analysis, FPCA)是函数型数据分析(Functional data analysis, FDA)中十分重要的方法,可用于函数型数据的降维及数据变化主要模式的探索。该程序包考虑的是二值函数型数据的FPCA,由于二值函数型数据来自离散分布,传统的FPCA方法将不再适用,对其的处理也具有一定的难度,我们发展了sparse logistic functional principal component analysis (SLFPCA)方法来对二值函数型数据进行主成分分析,该方法得到的主成分估计可揭示一定的局部稀疏特征,进而提高了结果的可解释性。
二、R程序包:SLFPCA
针对二值函数型数据,我们编写SLFPCA程序包的目的是:
1) 帮助使用者更加快捷地生成二值函数型数据,用于模拟试验等。
2) 利用SLFPCA方法对二值函数型数据进行主成分分析,同时所得主成分估计的局部稀疏性,可方便使用者对结果进行分析和解释。有关方法的详细内容请见论文《Sparse logistic functional principal component analysis for binary data》,链接:https://arxiv.org/abs/2109.08009。
SLFPCA软件包已经上传至CRAN官方服务器,并配有完整的功能帮助文档,内置的数据集可帮助使用者快速了解软件包的使用。
三、该程序包有什么特色?
1)实现对二值函数型数据的主成分分析
目前针对二值函数型数据主成分分析的研究还不是很充分,而实现相应分析的程序包更是少之又少。SLFPCA程序包则可以帮助使用者更加便捷地对二值函数型数据进行探索及分析。
2)结果的可解释性
在考虑二值函数型数据主成分分析的基础上,我们还希望所得的主成分估计具有一定的局部稀疏性,进而提高结果的可解释性。图1为将SLFPCA程序包中的SLFPCA()函数应用到一组运动数据上所得的结果,可以发现所得估计在某些子区间上取值严格等于0,这为我们探索数据的变化模式带来了很大的便利,详细的数据分析过程见https://arxiv.org/abs/2109.08009。
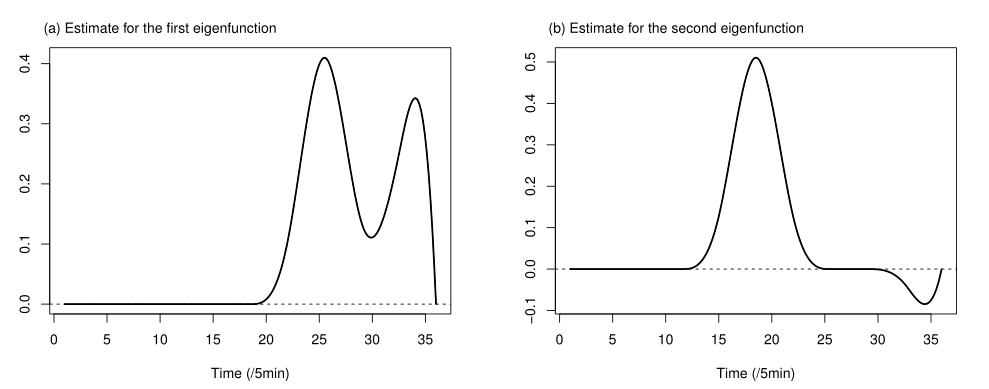
图1
