新闻动态
统计咨询介绍 | R程序包KFPCA:非高斯纵向数据的函数型主成分分析工具
时间:2021-10-01一、什么是KFPCA?
随着数据采集技术的提高,函数型数据在生物医学、环境监测、影像学等领域广泛出现。函数型主成分分析(Functional principal component analysis, FPCA)是函数型数据分析(Functional data analysis, FDA)中十分重要的方法,主要用于函数型数据的降维和揭示数据变化的主要模式。传统的FPCA方法是基于协方差函数进行的,这就导致其在数据偏离高斯假设时,表现不佳。而Kendall functional principal component analysis(KFPCA)是一种适用于非高斯情形的FPCA方法,不仅如此,该方法还可应用于稀疏取点的函数型数据或纵向数据。
二、R程序包:KFPCA
针对非高斯函数型/纵向数据,我们编写KFPCA程序包的目的是:
1)利用KFPCA方法对数据进行完整的主成分分析,包括特征函数的估计、主成分得分的估计及曲线的预测。有关方法的详细内容请见论文《Robust Functional Principal Component Analysis for Non-Gaussian Longitudinal Data》。
2)将KFPCA的部分子步骤写成单独的函数,包括提供局部线性估计中常用的核函数、GCV选择窗宽等等,以便使用者更加灵活地结合实际情况使用该软件包。
KFPCA软件包已经上传至CRAN官方服务器,并配有完整的功能帮助文档,内置的数据集可帮助使用者快速了解软件包的使用。
三、该程序包有什么特色?
1) 实现对非高斯函数型/纵向数据的主成分分析
通过软件包中的主函数KFPCA()可实现对数据的完整主成分分析,输出的结果包括特征函数的估计、主成分得分的估计、曲线的预测等内容,函数操作简单便捷。同时,我们还将KFPCA的部分子步骤单独写成函数,包括提供局部线性估计中常用的核函数、GCV进行窗宽的选择、计算均值函数的局部线性估计、最小二乘方法进行主成分得分的估计及预测。
2) 其他功能
KFPCA软件包还提供了其他功能,比如基于Karhunen–Loève展开生成所需的函数型/纵向数据,该功能可以帮助使用者更轻松地产生函数型模拟数据。同时,软件包还提供了实现函数型/纵向数据稀疏程度可视化所需的函数。图1的左右两图分别为利用软件包产生的两组模拟数据对应的稀疏程度图,我们可以很直观地看出右图对应的模拟数据比左图对应的模拟数据更加稀疏。
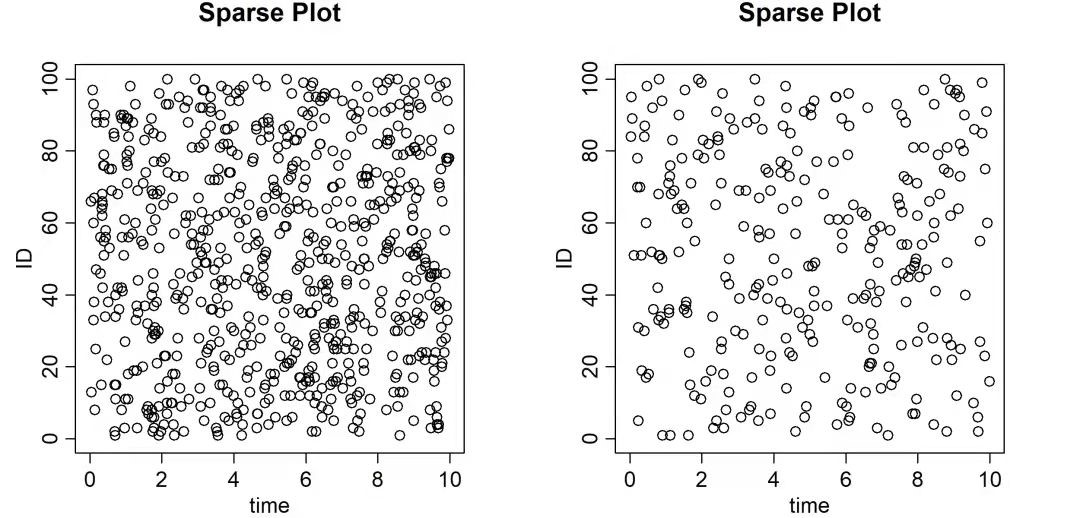
图1:数据稀疏程度图
